Area is one of the most basic fundamentals of geometry. When we first start to study geometry and shapes, we learn about perimeters, circumferences, areas and volumes. Of course, when we start to learn something, we start with the basics. In geometry, the basics are the simple shapes that we learn to recognize as children. Squares, circles, triangles, rectangles, and the various other shapes are fairly simple to understand. But, in the real world how often to we need to find the area of an exact circle, or a perfect square? In reality, it is more useful to know how to calculate the area of an irregular shape.
Irregular shapes are much more common than regular shapes. And, finding the area of regular shapes with accuracy is an important ability to have. The first example that I can think of is the layout of a home, or even a property. Real estate agents need to know how to calculate the floor space in a house, and the size of a parcel of land. It’s rare that either of these take the form of a perfect shape like a square, but with some practice and patience, you can use the formulas for simple shapes to determine the area of an irregular shape.
Look at this picture. You probably don’t recognize the shape. That’s because it is irregular. We’ll call it a problemogram. If you look closely, you can start to discern some of the properties of simple shapes.
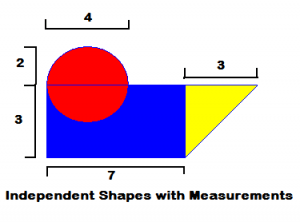
By breaking this large shape down into smaller shapes, we can calculate the areas of the seperate shapes and then add them to find the total of the larger shape. If you look at the illustration below, it will show some of the measurements of this larger shape.
By breaking this shape into a circle, rectangle, and triangle, we can calculate the independent areas of these shapes to determine the total of the original shape. Be careful about the circle. If you notice, half of the area of the circle overlaps with the rectangle and won’t be needed for the calculation.
So, we need to: 1. Calculate the area of the circle. 2. Calculate the area of the rectangle. 3. Calculate the area of the triangle. 4. Add all of the areas together and subtract half of the circle area that overlaps the rectangle.
By doing all of this, I get the following answers: Area of circle is 12.5664 square units. For the rectangle, I get 21 square units. And the for the triangle I calculate 4.5 square units. Add all of these together and you have about 38.07 square units. Don’t forget to subtract the overlapping half-circle and you will have an answer of about 31.8 square units for the total area of the irregular shape.
What other irregular shapes would this be useful for in real life?
Here are some online calculators that may be useful.
Hypotenuse Calculator (Pythagorean Theorem)
CalcuNATION is a website featuring online calculators and educational resources for mathematics. Other Mathematical Blogs ( CalcuNATION on EduBlogs and CalcuNATION on Blogger)