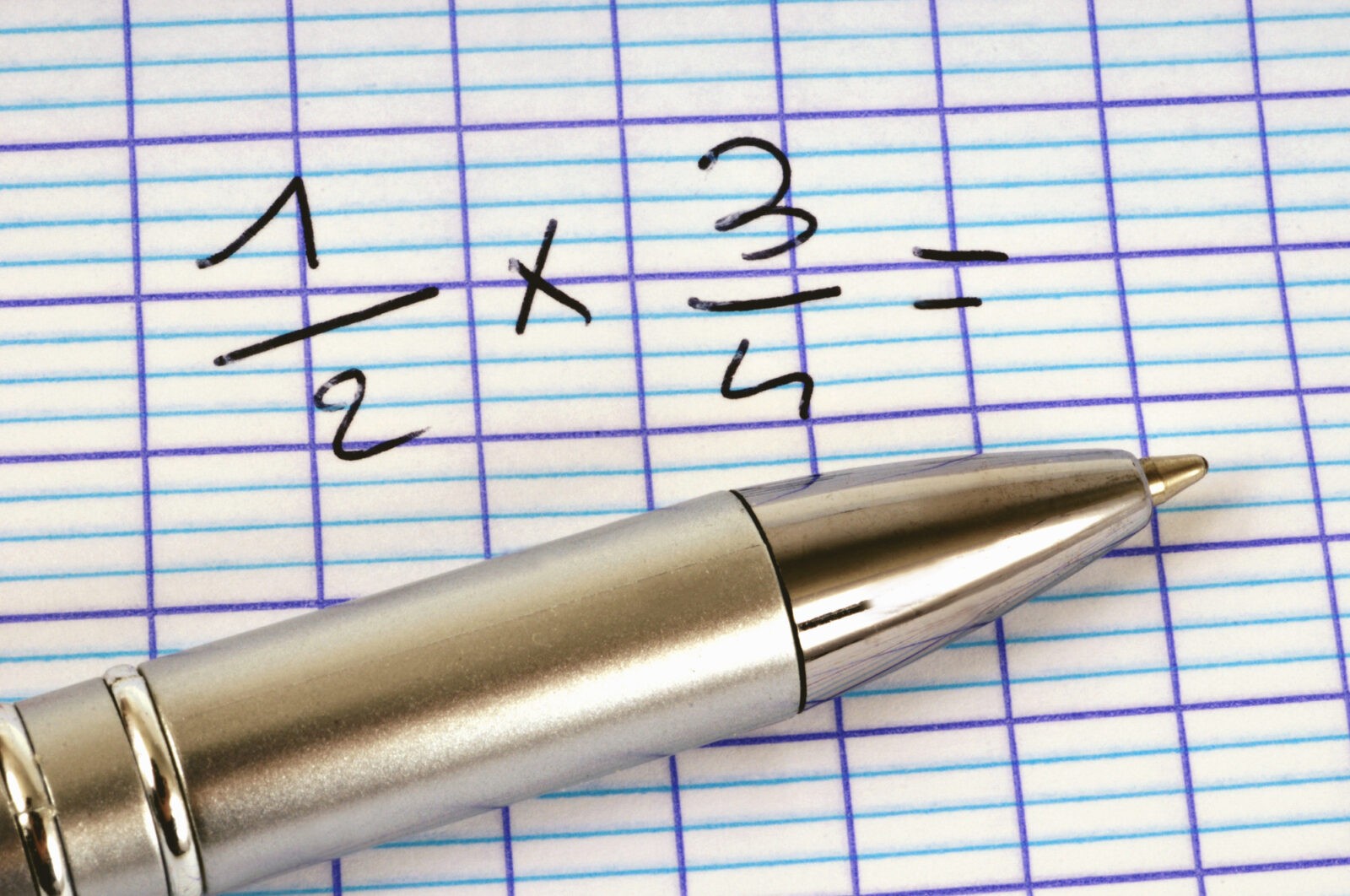Math doesn’t always come easy for everyone, especially when grade schools begin teaching algebra and fractions. While others excel in geometry, they could struggle with fractions.
Fractions tell us how many parts of a whole there are. A fraction has both numerators and denominators. This article will help you and your child understand fractions better and answer any questions they may have. Continue reading to learn how to do fractions!
1. Numerator and Denominators
When looking at a fraction, there are always numbers written on the top and bottom of the line. The number on top is the numerator; this defines the part of the whole we are talking about. When looking at the fraction 1/4, 1 is the numerator. This indicates that one is part of a whole with four parts.
The denominator is the number on the bottom half of the fraction. This number tells how many parts a “whole” is and represents the number of parts the whole divides into. A trick to remember the bottom is the denominator think “down”-ominator.
When looking at the fraction 1/4, 4 is the denominator. This means the whole divides into four equal parts.
2. Proper and Improper Fractions
There are three main types of fractions: Proper fractions, improper fractions, and mixed fractions. A proper fraction is where the numerator is smaller than the denominator. An improper fraction is where the numerator is larger than the denominator.
A fraction equals a number larger than one if it is improper. Keep in mind, you never want to write a final solution as an improper fraction. Simplify the fraction to make it a whole or mixed number, which we’ll go over how to do later.
Here are some examples of improper fractions: 10/3, 9/4, 15/3, 25/5.
3. Simplifying Fractions
In some cases, you may need to simplify an improper fraction. These fractions simplify into mixed or whole numbers – fractions that won’t divide evenly are mixed numbers.
The first step in simplifying an improper fraction is to divide the numerator by the denominator. We’ll use the fraction 10/3 as an example. The numerator in this fraction is 10, so we’ll divide 10 by 3.
3 goes into the number 10 three times with a remaining number of 1 – this is the remainder. Using the same denominator, write the remainder as a fraction. Since the remainder number is 1, the fraction is 1/3.
The original fraction of 10/3 now becomes a mixed number of 3 1/3. Remember, not all improper fractions will become mixed numbers. Some will divide evenly into whole numbers. Example: 25/5 simplifies to a whole number of 5.
4. Equivalent Fractions
Equivalent fractions are like simplified fractions in that they appear different until they are reduced to their simplest forms. Though we are simplifying fractions, we won’t be turning them into proper or improper fractions.
An example of an equivalent fraction is 10/20. This can be simplified not once but twice into 5/10 and 1/2. All three are equivalent fractions.
5. Finding the Greatest Common Factor
The greatest common factor (GFC) is the largest factor which divides two numbers and is used when you want to reduce or simplify a fraction. This is found by figuring out what prime numbers are multiplied together to make up each number.
Prime numbers are numbers which can only be divided by one or itself. Some examples are: 1, 2, 3, 5, 7, 11, and 13. We’ll use the fraction 12/60 as an example.
By finding the common denominator we are dividing the fractions into smaller sizes until they are the same size. Some fractions have many common denominators, but most prefer to find the smallest one.
Let’s break down the fraction 12/60 into individual small factors. The factors of 12 are 2x2x3; the factors of 60 are 2x2x3x5. What common factors do you see?
Both sets have 2x2x3, which when multiplied together, equal 12. Now we know the GCF is 12, and if put into it’s simplest form, is reduced to 1/5.
6. Finding the Lowest Common Denominator
Now that we know how to find the GFC, we’ll learn how to find the lowest common denominator (LCD). The easiest way to find the common denominator is to multiply both denominators together. In this case, we’ll use 5/6 and 3/8 as examples. Multiplying 6×8 gives us 48 as the common denominator.
Because we multiplied the denominators by each other, we will also multiply the numerator by the same numbers. This gives us new fractions of 40/48 and 18/48. Now that we have the same denominator, we need to see if we can find the LCD. To do this we’ll look at the factors of both 6 and 8.
We learned how to do this with GCF. The factors of 6 are 2×3 and the factors of 8 are 2x2x2. We see that 6 and 8 have the common factors of 2. We’ll multiply 2x2x2x3 to get the lowest common denominator of 24.
7. How to Add and Subtract Fractions
Now that we’ve learned the basics about fractions it’s time to start adding and subtracting them. To add fractions, they have to have the same denominators.
To do this, find the lowest common denominator using the steps above and change each fraction to an equivalent fraction. Once you find the LCD, add or subtract the numerators like normal and put the final number over the denominator. Reduce the fraction to its simplest form.
8. How to Multiply
Multiplying and dividing fractions sounds intimidating, but it’s actually really easy! Before you start multiplying, you’ll want to make sure each fraction is in its lowest or simplest terms.
Once you do that, multiply the numerators and denominators across. Now that you have a new fraction, simplify it again by reducing it to it’s lowest terms.
9. Changing Mixed Numbers to Improper Fractions
As we mentioned earlier, it’s always a good idea to convert an improper fraction into a mixed number. Yet, it’s hard to work with them and other fractions together. In these cases, it’s better to convert them back into improper fractions before moving on.
Converting a mixed number is easy once you understand how to add fractions. We’ll use 2 4/5 as an example. To convert this to an improper fraction start by writing it as 2/1 and 4/5.
Since 5 is the common denominator, we’ll multiply 2/1 by 5/5 creating a fraction of 10/5. Now that we common fractions, we’ll add the numerators to create an improper number.
How To Do Fractions
Fractions are a stepping stone in understanding harder math and algebra. You’ll want to make sure you fully comprehend how to do fractions before moving on to other math classes.
To see how the process works or if you’re having trouble with the steps above, check out our fraction calculator! For other math-related topics browse our website.