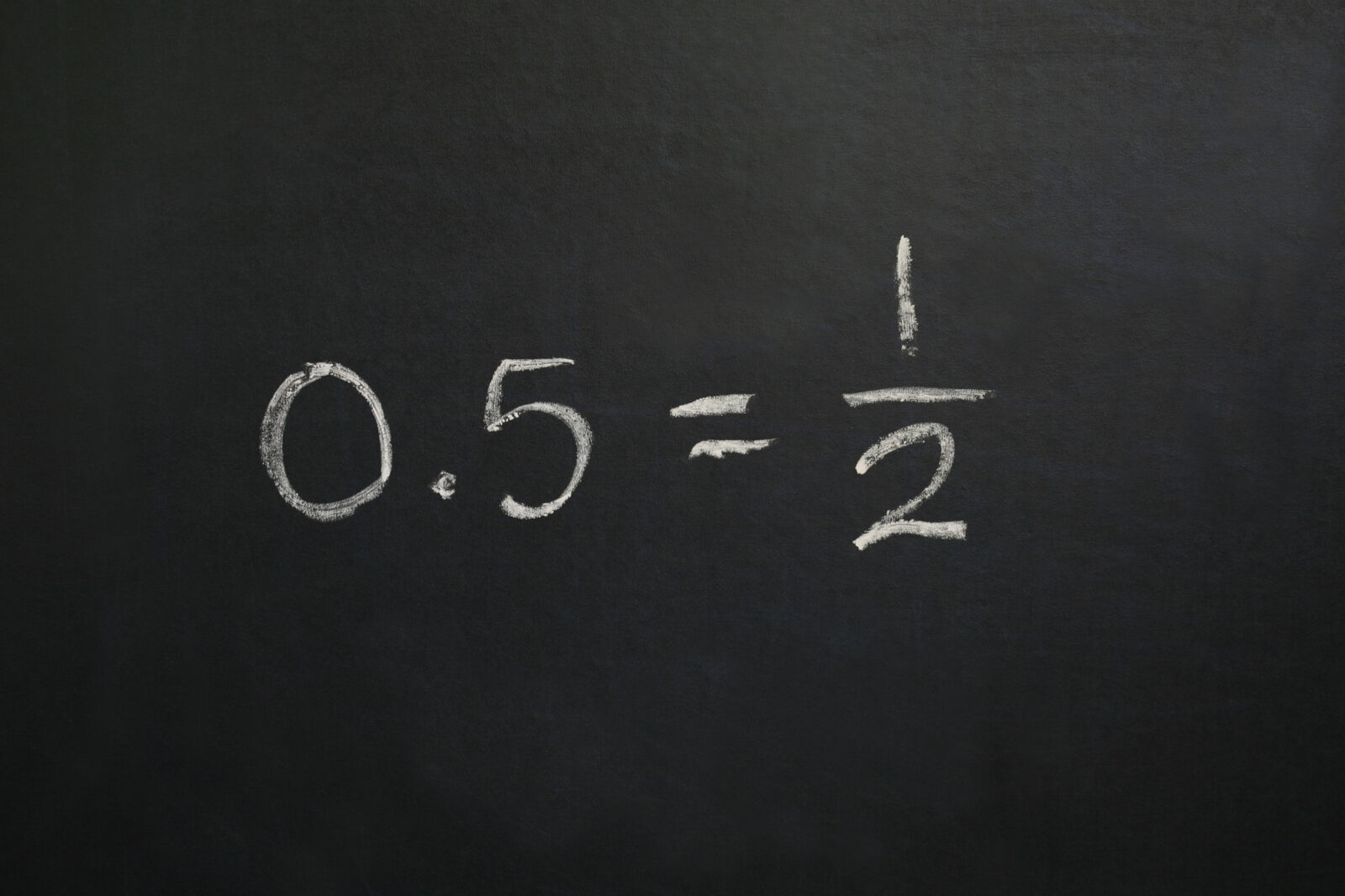Converting decimals to fractions isn’t something you only do in a classroom.
There are multiple different circumstances in your everyday life that might require this kind of knowledge. For example, you might need to know how to convert decimals and fractions when you’re looking for the cheapest can of beans per ounce at the grocery store.
Take a look at this guide to learn how you can convert decimals into fractions in three simple steps.
How to Convert a Decimal to a Fraction
You can convert any type of decimal to a fraction, even the messy ones. And the same is true for fractions. All fractions have a decimal equivalent, and all decimals have a fraction equivalent.
Converting decimals to fractions isn’t as hard as you think. All you need are the right steps.
There are two different types of decimals: terminate decimals and repeating decimals. When converting these decimals to fractions, they each need their own method.
Here’s a quick breakdown of how to convert terminate and repeating decimals.
Terminate Decimal
Terminate decimals are decimals that have an end. An example might be something like .2, .2376, and .854. Each of these decimals has a limited number of digits. These are the most common type of decimals, and they are the easiest to convert.
So let’s say you’re trying to convert the decimal .88. Here’s how you start.
Step One: To get started, write the decimal as a fraction. This will always involve putting the decimal over 1. When you’re done, it should look like this: 88/1.
Step Two: Once you’ve written the decimal as a fraction, you have to multiply both the top and the bottom by 10, 100, 1,000, 10,000, etc. In other words, you want to multiply the decimal by as many zeros as there are digits to the left of the decimal point.
In our example, .88 has two digits to the left of the decimal point. Because of this, we’ll multiply the top and bottom of .88/1 by 100.
After this, we’ll end up with 88/100.
Step Three: Now we have to reduce the fraction as low as it can go. You can reduce both the top and the bottom of the fraction 88/100 by 4. Once reduced, the fraction becomes 22/25.
Because you can’t reduce this fraction any farther, this is the fraction equivalent of .88.
Repeating Decimal
Unlike a terminate decimal, repeating decimals are decimals that have no end. Of course, you can’t write out a decimal that never ends. So instead, you can round the decimal off at the end or write it with a bar covering the last repeating digit.
For example, you can round the repeating decimal .888888 to 888889. Or you could write .8 with a bar over the 8.
Step One: To start the equation, you need to let x equal your rounding decimal. So in this case, x=.888889.
Step Two: Next, you want to get one of the repeating digits onto the left side of the decimal point. For our example, we only have to multiply the decimal by 10.
In other words, 10x=8.88889.
In some cases, a repeating decimal might have more than one repeating number. You would have to multiply the decimal .467467467467 by 100 to get all of the repeating numbers onto the left side of the decimal point. When you’re done, your decimal would become 467.467467467.
Step Three: Write another equation where x equals the decimal with the repeating digit to the right of the decimal point. For our example, this second equation would be x=.888889.
Step Four: Now all you have to do is solve for x. Here’s what the entire equation looks like when you put it all together.
10x-x=8.88889-.888889.
Start by subtracting both sides of the equation.
9x=8
Divide both sides of the equation by 9 so the x stands by itself.
x=8/9
In this case, you can’t reduce the fraction any lower than it already is. The fraction equivalent to .888889 equals 8/9.
How to Convert a Fraction to a Decimal
To convert a fraction back to a decimal, you have to do some division. Let’s take a look at the fraction 3/5. When you divide the number 3 by the number 5, you end up with a decimal of .6.
It’s as simple as that.
The fastest and easiest way to convert fractions back to decimals is to use a calculator. All you have to do is press a few buttons and you have your answer.
Common Decimals You Should Know
There are a lot of common decimals you’ll come across in the world of math. Memorizing some of these will allow you to do these conversions in a single glance. This can be helpful if you’re doing some basic math and don’t have a calculator on hand.
Here’s a quick list of common decimals and their fraction equivalents.
- 1/32=0.03125
- 1/16=0.0625
- 9/10=0.9
- 7/10=0.7
- 3/10=0.3
- 1/10=0.1
- 8/9=0.8888
- 7/9=0.7777
- 5/9=0.5555
- 4/9=0.4444
- 2/9=0.2222
- 1/9=0.1111
- 7/8=0.875
- 5/8=0.625
- 3/8=0.375
- 1/8=0.125
- 5/6=0.8333
- 1/6=0.16667
- 4/5=0.8
- 3/5=0.6
- 2/5=0.4
- 1/5=0.2
- 3/4=0.75
- 1/4=0.25
- 2/3=0.6666
- 1/3=0.3333
- 1/2=0.5
While you might not be able to memorize all of these decimals and fractions, it can make solving math problems a bit quicker.
What You Need to Know About Converting Decimals to Fractions
When you’re converting decimals to fractions, the first thing you need to do is figure out what kind of decimal you’re dealing with. Remember, a terminate decimal is a decimal with a limited number of digits. A repeating decimal goes on forever.
Once you know what kind of decimal you have, you can convert it to a fraction using one of the two methods.
If you want to convert a fraction back to a decimal, you have to divide the number on the top of the fraction by the number on the bottom of the fraction. The easiest way to do this is with a calculator, but you can use long division as well.
Are you looking for a good calculator you can use while doing your finances? Take a look at some of these options.